2182. Lost Cows

N (2 ≤ N ≤ 8,000) cows have unique brands in the range 1..N. In a spectacular display of poor judgment, they visited the neighborhood 'watering hole' and drank a few too many beers before dinner. When it was time to line up for their evening meal, they did not line up in the required ascending numerical order of their brands.

Regrettably, FJ does not have a way to sort them. Furthermore, he's not very good at observing problems. Instead of writing down each cow's brand, he determined a rather silly statistic: For each cow in line, he knows the number of cows that precede that cow in line that do, in fact, have smaller brands than that cow.

Given this data, tell FJ the exact ordering of the cows.

Input.

* Line 1: A single integer, N

* Lines 2..N: These N-1 lines describe the number of cows that precede a given cow in line and have brands smaller than that cow. Of course, no cows precede the first cow in line, so she is not listed. Line 2 of the input describes the number of preceding cows whose brands are smaller than the cow in slot #2; line 3 describes the number of preceding cows whose brands are smaller than the cow in slot #3; and so on.

Output.

* Lines 1..N: Each of the N lines of output tells the brand of a cow in line. Line #1 of the output tells the brand of the first cow in line; line 2 tells the brand of the second cow; and so on.

Sample Input

5

1

2

1

0

Sample Output

2

4

5

3

1

РЕШЕНИЕ

дерево отрезков

Анализ алгоритма

Пусть массив in содержит входные данные: in[i] равно числу коров, стоящих перед i-ой и имеющих номера меньше чем у i-ой коровы. При этом in[1] = 0.

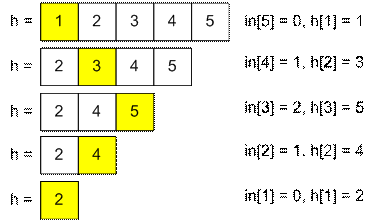
Пусть h = {1, 2, …, n} – отсортированный массив высот. Тогда алгоритм построения требуемой перестановки res следующий:

for i = n, n - 1, …, 2, 1

res[i] = h[in[i] + 1];

удалить h[in[i] + 1];

Осталось подобрать структуру данных, при помощи которой можно промоделировать работу массива h.

Пусть b – массив целых чисел, занесем во все его ячейки единицы: b₁ = b₂ = .. = b_n = 1. Построим по нему дерево отрезков.

Реализация алгоритма

#include <cstdio>

#include <algorithm>

#define MAX 8010

using namespace std;

int SegTree[4*MAX], in[MAX], m[MAX];

int i, n;

void BuildTree(int v, int Left, int Right)

{

if (Left == Right) SegTree[v] = 1;

else

{

int Middle = (Left + Right) / 2;

BuildTree(v*2, Left, Middle);

BuildTree(v*2+1, Middle+1, Right);

SegTree[v] = SegTree[v*2] + SegTree[v*2+1];

}

}

int Get(int v, int LeftPos, int RightPos, int Value)

{

if (LeftPos == RightPos) return LeftPos;

int Middle = (LeftPos + RightPos) / 2;

if (SegTree[2*v] > Value)

return Get(2*v,LeftPos,Middle,Value);

else

return Get(2*v+1,Middle+1,RightPos,Value - SegTree[2*v]);

}

void update(int v, int LeftPos, int RightPos, int Position, int NewValue)

{

if (LeftPos == RightPos) SegTree[v] = NewValue;

else

{

int Middle = (LeftPos + RightPos) / 2;

if (Position <= Middle) update (v*2, LeftPos, Middle, Position, NewValue);

else update (v*2+1, Middle+1, RightPos, Position, NewValue);

SegTree[v] = SegTree[v*2] + SegTree[v*2+1];

}

}

int main(void)

{

scanf("%d",&n);

BuildTree(1,1,n);

in[1] = 0;

for(i = 2; i <= n; i++)

scanf("%d",&in[i]);

for(i = n; i >= 1; i--)

{

m[i] = Get(1,1,n,in[i]);

update(1,1,n,m[i],0);

}

for(i = 1; i <= n; i++)

printf("%d\n",m[i]);

return 0;

}